Gravure Melancholia I / 24 x 19 cm
Albrecht Dürer (1471-1528) est généralement considéré comme l'artiste Allemand le plus célèbre de la Renaissance. Il était d'environ 20 ans plus jeune que Leonard de Vinci et autour de 1500 il est devenu beaucoup intéressé à la relation entre les mathématiques et l'art. Leonardo et son contemporain, le mathématicien Pacioli, ont presque certainement influencé Dürer dans ces études. En 1514 il a créé la gravure sur cuivre du nom de "Melancholia I", qui contient son carré magique - le premier carré magique publié en Europe.
Cette gravure sur cuivre par Albrecht Dürer a été vu comme un portrait de l'artiste et l'essence de l'humanisme allemand. La figure avec ailes illustre simultanément les dangers et les satisfactions de l'activité intellectuelle. C'est l'image de l'esprit créatif de l'homme seul avec ses pensées intérieures. L'échelle appuyée contre le bâtiment, indiquant que ce n'est pas fini, le problème non résolu de géométrie, l'amour au-dessus d'une roue, le chien hydrophobe, la chute de sable dans sablier, et le solde oscillant vide ... tous résument ce désespoir à mélancholie.
 Carré de Dürer dans la gravure |
 Albrecht Dürer (auto-portrait à 28 ans) |
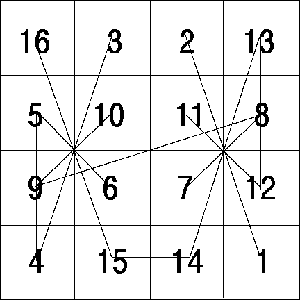
Le carré magique de Dürer, le plus connu et le plus énigmatique, est un carré magique de constante magique 34, utilisé dans une gravure intitulée Melancholia I par Albrecht Dürer (The British Museum, Burton 1989, Gellert et al. 1989). La gravure montre un enchevêtrement désordonné d'équipement scientifique et un intellectuel qui est absorbé dans ses pensées. Le carré magique de Dürer est situé dans le coin supérieur droit de la gravure. Les numéros 15 et 14 apparaissent dans le milieu de la rangée du bas, indiquant la date de la gravure, 1514.
La somme 34 peut être trouvé dans les lignes, les colonnes, les diagonales, chacun des quadrants, les quatre carrés du centre, les carrés en coin, les quatre nombres extérieurs, au sens des aiguilles d'une montre à partir des coins (3+8+14+9), de même que les quatre nombres au sens anti-horaire, les deux séries de quatre nombres symétriques (2+8+9+15 et 3+5+12+14) et la somme des deux entrées centrales des deux colonnes et des deux lignes externes (i.e. 5+9+8+12), ainsi que plusieurs quatuors en forme de cerf-volant, par exemple, 3+5+11+15. En fait, il y a 86 différentes combinaisons de quatre nombres dans le carré de Dürer donnant la somme magique 34!
Dans l'applet ci-dessous, les nombres sont reproduits dans un style plus moderne. Chaque rangée, chaque colonne et chaque diagonale donne la somme 34; ce sont les propriétés magiques traditionnelles. Mais il y a plus de magie à trouver ici. Il y a effectivement treize façons de diviser ce carré en quatre groupes de quatre cellules, avec chaque groupe de quatre cellules donnant la somme 34. Le menu de l'applet permet d'en sélectionner. Si vous cliquez sur une des cellules, les nombres du groupe seront élargis et mis en relief en rouge. Les regroupements de cellules ne sont pas arbitraires. Les positions dans le carré de Dürer peuvent être perçues comme un espace vectoriel fini, dans lequel chaque série de quatre groupes à quatre cellules est une série de plans parallèles.
Le carré magique de Dürer a la propriété que les sommes dans l'un des quatre quadrants, ainsi que la somme des quatre nombres du milieu, sont toutes 34 (Hunter et Madachy 1975, p. 24). Il s'agit donc d'un gnomon carré magique. Un gnomon est un carré magique 4 × 4 carré magique dans lequel les éléments, dans chaque coin 2 × 2 ont la même somme. Le carré magique de Dürer, illustré ci-dessus, est un exemple d'un gnomon carré magique car les sommes dans chacun des quatre quadrants (ainsi que la somme des quatre nombres du milieu) sont toutes de 34. En outre, toute paire de nombres placés de façon symétrique par rapport au centre du carré conduit à la somme 17, une propriété qui rend le carré encore plus magique.
L'échange de colonnes ne change pas la somme de colonnes ou la somme de lignes. Il y a habituellement modification de la somme de diagonale, mais dans ce cas, les sommes de diagonales sont encore de 34. Dès lors notre carré magique correspond à l'un dans la gravure de Dürer. Dürer a probablement choisi ce carré particulier 4 x 4 car la date de réalisation, 1514, se retrouve dans le milieu de la rangée du bas.
Les huit figures du carré magiques de Dürer sont représentées ci-dessus. Rappelons que tout carré magique possède huit "formes" ou huit "figures" différentes, obtenues par rotations (4 figures, y compris l’original), symétrie par rapport aux médianes (2 figures) et symétrie par rapport aux diagonales principales (2 figures).
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Original | Rotation ¼ |
Rotation ½ | Rotation ¾ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Symétrie 1ère médiane | Symétrie 2e médiane |
Symétrie 2e diagonale | Symétrie 1ère diagonale |
Cette section présente quelques résultats drôles soulignés par David Bowman.
L'année de la gravure est inscrit 15-14, dans les cellules centrales de la rangée du bas. Plus encore, le nombre de droite est de 1 est le même que A dans un simple codage maçonnique de valeurs-lettres [A=1, B=2, C=3, ... Z=26], et le nombre de gauche de la date est de 4, soit la valeur guématrique de D. Les deux nombres sont donc inter-changeables avec les lettres A et D, presque religieusement utilisées comme monogramme d'Albrecht Durer.
La somme de tous les nombres dans le carré magique de Dürer est 136, et ce nombre cache à la fois le maître et le titre de l'oeuvre. Dürer a utilisé une autre variante, latine, de l'orthographe de son nom - ALBRECHT DVRER:
Il existe également une autre blague mathématique cachée dans les chiffres. Si les cellules, deux à deux, sont prises pour un nombre unique (16 et 3 = 163, 2 et 13 = 213, 5 et 10 = 510, et ainsi de suite) et si on additionne le tout, la valeur 2368 est obtenue. Ce chiffre est significatif car il est égal à la valeur de Jésus-Christ en grec:
Les dimensions de la gravure de Dürer sont d'environ 18.9 x 24.1 cm, ce qui est très proche de la proportion de 11:14. Ce ratio a été très souvent utilisé dans les compositions classiques, surtout parce qu'elle est dérivée du ratio 22:7, très proche de Pi = 3,14159 ... et il était connu depuis les temps anciens. L'importance de Pi pour la composition de Melencolia I est souligné par la sphère dans le coin inférieur gauche de la gravure, qui est en même temps aussi un module de la composition.
La constante magique d'un carré magique normal ne dépend que de n et a la valeur M = (n3 + n)/2. Voici la preuve. Étant donné un carré magique normal 
, supposons que M est le nombre-somme auquel devrait correspondre le total de chaque rangée, colonne et diagonale. Comme il y a n lignes, la somme de tous les nombres dans le carré magique doit être 
. Mais les nombres additionnés sont 1, 2, 3, ... + n2, et ainsi 1 + 2 + 3 + ... + n2 = . En notation sommation, 
. En utilisant la formule de cette somme, nous avons 
, et la résolution de M donne 
. Ainsi, un carré magique normal Lo Shu 
doit avoir ses lignes, colonnes et diagonales totalisant 
, un d'Albrecht Dürer 
de M = 34, un de Benjamin Franklin 
de M = 260, et ainsi de suite.
L'inventaire des éléments présents dans la gravure inclut une vingtaine d'articles, tous aisément identifiables :
Le carré figurant dans la Melencholia est un type particulier de carré magique: la somme dans l'un de ses quatre quadrants, ainsi que la somme des nombres du carré du milieu, valent également 34, la valeur magique du carré. C'est un carré magique gnomon. Ce carré devrait être une influence bénéfique contre la mélancolie. Au milieu de la dernière ligne, les nombres 15 et 14 qui correspondent à la date de la gravure, 1514; c’est aussi la date de la mort de Barbara, la mère d’Albrecht Dürer.
La gravure Melancholia I, montre un penseur frustré, assis devant un polyèdre rare. Melencolia a été l'objet d'un nombre considérable d'études. La suggestion qu'une série de gravures sur le sujet était prévue n'est généralement pas acceptée. Au contraire, il semble plus probable que le «I» réfère à la première des trois types de mélancolie définis par l'écrivain allemand Cornelius Agrippa. Dans ce type, Melencholia Imaginativa, les artistes sont soumis à une «imagination» qui l'emporte sur «l'esprit» ou la «raison».
Erwin Panofsky (Juif Allemand et historien de l'art) propose l'interprétation la plus autoritaire de Melencolia I, soit celle d'un "auto-portrait spirituel" de Dürer. Patrick Doorly a suggéré que Melencolia I serait l'illustration de l'échec à définir la beauté tel que Platon l'a décrite dans son dialogue Hippias Majeur. Il serait même encore plus redevable au livre De Divina Proportia de Luca Pacioli. John Read a fait des observations sur le symbolisme alchimique de la gravure. Louis Barmont a écrit une étude sur l'ésotérisme de la Mélencolia intitulé : « L'ésotérisme d'Albert Dürer, la Mélencolia » (1947), dans laquelle on trouvera des éléments sur l'appartenance de Dürer à des sociétés d'ésotérisme chrétien de son temps.
L'animal couché au pied du grand ange est un lévrier, veltro en italien. Selon L. Barmont, cet animal, associé à la signature numérique du 515 (le Cinq-Cent-dix-et-cinq) figure dans la Divine Comédie de Dante, et on l'associe à certains éléments apocalyptiques. La Balance exprime classiquement une notion de "jugement", qui serait ici en relation avec un jugement de nature apocalyptique, étant donné la présence des autres éléments de la gravure. La balance est située près près du petit ange, pour l'instant en sommeil. L'échelle est souvent associée aux sept Arts libéraux, qui sont en relation avec l'hermétisme. Sur la nature hermétique de la gravure, on remarquera la présence d'un creuset alchimique, juste à côté du polyèdre. Le sablier est bien évidemment une figuration de l'écoulement du temps, et cet élément renforce la posture d'attente qui semble baigner le monde angélique du premier plan. Toutefois il est représenté au moment où les deux bulbes sont également remplis, suggérant plutôt un certain équilibre statique comme celui de la balance à sa gauche ou la cloche à droite.