Benjamin Franklin (1706-1790), American scientist, inventor, statesman, philosopher, economist, musician, and printer, invented this 8x8 magic square in his spare time. It is a pure magic square in that it utilizes the consecutive counting numbers from 1 to 64. Moreover, Franklin 8×8 Square is a panmagic square having magic constant 260.
The animation below shows the combinations, I have found so far, that sum to 260. The combinations will amaze you ... really magic!!! As Ben himself remarked famously, the 16 by 16 square is "the most magically magical of any square ever made by any magician." (Jared Sparks, ed., The Works of Benjamin Franklin Vol. VI, 1856).
Describing his invention in 1771, Franklin stated, "I was at length tired with sitting there to hear debates, in which, as clerk, I could take no part, and which were often so unentertaining that I was induc'd to amuse myself with making magic squares or circles" (Franklin's Autobiography, 1793).
|
|
| Franklin's Pure Magic Square | Benjamin Franklin |
A Franklin magic square is a semi-magic square with each of the four main bent row sums equal to the magic constant. All the rows and columns sum to the number 260 [260 = 22x5x13], but that is not all. Half rows and half columns sum to 130. The four entries in every 2x2 subsquare sum to 130. But there is even more! Instead of requiring diagonal sums to be constant (as in a fully magic square), Franklin used "bent rows" such as those highlighted below. Franklin preferred to measure ‘magic’ using a different kind of diagonal from his predecessor Frénicle (B. Frénicle de Bessy, et al., Divers ouvrages de mathematique et de physique (1693)), employing a shape which he called a "bent row."
V-shapes can be taken sideways or even upside-down, and they will still sum to 260. Each half-row and half-column sums to 130, and all of the parallel bent rows sum to 260. He notes, “The four corner numbers, with the four middle numbers, make 260.” Also, any 2 x 2 block adds up to 130 and the twelve disconnected bent rows add up to 260. In the figures below, the bent diagonals going from top to bottom (Figure 1) sum to 260. Even the broken ones that have two pieces! Follow the colored patterns and you will be able to check this. (Each bent diagonal or broken diagonal should have 8 cells.) The other three figures show the other diagonals going from from right to left (Figure 2), from bottom to top (Figure 3) and from left to right (Figure 4) also have sums of 260.
 |  |
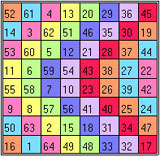| Figure 1 | Figure 2 |
 |  |
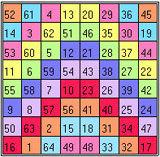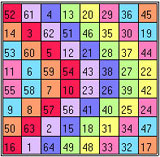| Figure 3 | Figure 4 |
The magic constant of a normal magic square depends only on n and has the value M = (n3 + n)/2. Here is the proof. Given an 
normal magic square, suppose M is the number that each row, column and diagonal must add up to. Then since there are n rows the sum of all the numbers in the magic square must be 
. But the numbers being added are 1, 2, 3, ... n2, and so 1 + 2 + 3 + ... + n2 = . In summation notation, 
. Using the formula for this sum, we have 
, and then solving for M gives 
. Thus, a Lo Shu's 
normal magic square must have its rows, columns and diagonals adding to 
, a Albrecht Dürer's 
to M = 34, a Benjamin Franklin's 
to M = 260, and so on.
This section is based on an article by C.A.J. Hurkens, Plenty of Franklin Magic Squares, but none of order 12, June 4, 2007.
There is crazy theory behind Franklin Magic Square. According to various descriptions, a natural Franklin Magic Square of even size n is a square matrix M with n rows and columns with the properties:
According to Hurkens, it turns out that any Franklin Magic Square maintains its magic properties under a number of matrix transformations, namely:
Here's an amusing passage from Benjamin Franklin's autobiography:
"Being one day in the country at the house of our common friend, the late learned Mr. Logan, he showed me a folio French book filled with magic squares, wrote, if I forget not, by one M. Frenicle [Bernard Frenicle de Bessy], in which, he said, the author had discovered great ingenuity and dexterity in the management of numbers; and, though several other foreigners had distinguished themselves in the same way, he did not recollect that any one Englishman had done anything of the kind remarkable. I said it was perhaps a mark of the good sense of our English mathematicians that they would not spend their time in things that were merely 'difficiles nugae', incapable of any useful application."
Logan disagreed, pointing out that many of the math questions publically posed and answered in England were equally trifling and useless. After some further discussion about how things of this sort might perhaps be useful for sharpening the mind, Franklin says. After seeing Ben's square, his friend, James Logan, refers to it as “the most magically magical of any magic square ever made by any magician.”
"I then confessed to him that in my younger days, having once some leisure which I still think I might have employed more usefully, I had amused myself in making these kind of magic squares..."
As explained by Franklin, each row and column of the square have the common sum 260. Also, he noted that half of each row or column sums to half of 260. In addition, each of the "bent rows" (as Franklin called them) have the sum 260. The "bent rows" are patterns of 8 numbers with any of the shapes and orientations shown below
It isn't clear from his verbal description whether Franklin was claiming just the five parallel patterns of each of these types that fall strictly within the square, or if he was claiming all eight, counting those that "wrap around". In any case, his square does possess this property. For example, if we shift the first "bent row" to the left, wrapping the ends around, we have the patterns.
In addition, Franklin noted that the "shortened bent rows" plus the "corners" also sum to 260. As with the previous patterns, this template can be rotated in any of the four directions, and shifted parallel into any of the eight positions (with wrap-around), and the sum of the highlighted numbers is always 260.
Finally, Franklin noted that the following two sets of eight numbers also sum to 260. He doesn't explicitly mention it, but these patterns can also be translated (with wrap-around), and since they are symmetrical between horizontal and vertical, they can be translated in either direction.